7. Unterrichtsblock

Kursinhalte

Maschinelles Lernen
Mittelwert, Median, Modus
Standardabweichung
Varianz
Perzentil

Maschinelles Lernen

Durch maschinelles Lernen lernt der Computer durch das Studium von Daten und Statistiken.
Maschinelles Lernen ist ein Schritt in Richtung künstlicher Intelligenz (KI).
Maschinelles Lernen ist ein Programm, das Daten analysiert und lernt, das Ergebnis vorherzusagen.

Datensätze

Für einen Computer ist ein Datensatz jede Sammlung von Daten. Dies kann jede Art von Datensammlung sein, von einem Array bis hin zu einer vollständigen Datenbank.

Beispiel für ein Array:

zahlen = [28, 64, 22, 48, 64, 61, 41, 61, 28, 46, 63, 39, 37, 45, 40]

Wenn wir uns das Array ansehen, können wir vermuten, dass der Durchschnittswert wahrscheinlich bei etwa 30 oder 40 liegt, und wir sind auch in der Lage, den höchsten und den niedrigsten Wert zu bestimmen, aber was können wir sonst noch tun?

Beispiel einer Datenbank:

Frucht	Herkunftsland	Preis (in Euro)	Erntesaison
Apfel	Deutschland	0,75	August – Oktober
Banane	Ecuador	1,20	Ganzjährig
Erdbeere	Spanien	0,50	Mai – Juni
Orange	Spanien	1,00	November – März
Kiwi	Neuseeland	1,80	Juni – Oktober
Ananas	Costa Rica	2,30	Ganzjährig
Weintraube	Italien	1,50	August – September
Wassermelone	Spanien	0,90	Juni – August
Mango	Indien	1,75	April – Juli
Kirsche	Türkei	0,03	Juni – Juli

Und wenn wir uns die Datenbank ansehen, sehen wir, dass die meisten Früchte aus Spanien kommen und die teuerste Frucht die Ananas ist. Aber was wäre, wenn wir vorhersagen könnten, zu welcher Jahreszeit die Vitaminaufnahme einer Bevölkerung am höchsten ist, indem wir einfach die anderen Werte betrachten?

Dafür ist maschinelles Lernen da! Daten analysieren und das Ergebnis vorhersagen!

Datentypen

Um Daten zu analysieren, ist es wichtig zu wissen, mit welcher Art von Daten wir es zu tun haben.

Wir können die Datentypen in drei Hauptkategorien einteilen:

Numerisch
Kategorisch
Ordinal

Numerische Daten
sind Zahlen und können in zwei numerische Kategorien unterteilt werden:

Diskrete Daten
– gezählte Daten, die auf Ganzzahlen beschränkt sind. Beispiel: Die Anzahl der vorbeifahrenden Autos.
Kontinuierliche Daten
– Messdaten, die eine beliebige Zahl sein können. Beispiel: Der Preis eines Artikels oder die Größe eines Artikels

Kategoriale Daten
sind Werte, die nicht miteinander verglichen werden können. Beispiel: ein Farbwert oder beliebige Ja/Nein-Werte.

Ordinaldaten
ähneln kategorialen Daten, können jedoch miteinander verglichen werden. Beispiel: Schulnoten, bei denen 1 besser ist als 2 und so weiter.

Wenn wir den Datentyp der Datenquelle kennen, können wir bestimmen, welche Technik wir bei der Analyse verwenden müssen.

Mittelwert, Median und Modus

Was können wir aus der Betrachtung einer Zahlengruppe lernen?

Beim maschinellen Lernen (und in der Mathematik) interessieren uns oft drei Werte:

Mittelwert – Der Durchschnittswert
Median – Der Mittelwert
Modus – Der häufigste Wert

Median:

Entscheidungsbäume: Der Median wird häufig in Entscheidungsbäumen verwendet, um den besten Spaltpunkt für die Aufteilung der Daten zu finden.
Anomalieerkennung: Der Median kann verwendet werden, um Anomalien in Datensätzen zu finden, da diese oft deutlich vom Median abweichen.
Robustheit: Der Median ist robuster gegenüber Ausreißern als der Mittelwert, was ihn in einigen Anwendungen nützlicher macht.

Modus:

Textanalyse: Der Modus kann verwendet werden, um die häufigsten Wörter oder Phrasen in einem Text zu finden.
Bildverarbeitung: Der Modus kann verwendet werden, um die häufigste Farbe in einem Bild zu finden.
Clusteranalyse: Der Modus kann verwendet werden, um Cluster von Datenpunkten zu finden, die ähnliche Eigenschaften haben.

Mittelwert:

Regression: Der Mittelwert wird häufig in der Regression verwendet, um die Beziehung zwischen zwei Variablen zu modellieren.
Klassifikation: Der Mittelwert kann verwendet werden, um Datenpunkte in verschiedene Klassen einzuteilen.
Optimierung: Der Mittelwert kann verwendet werden, um die optimale Lösung eines Problems zu finden.

Weitere Anwendungsbereiche:

Empfehlungssysteme: Der Median, Modus und Mittelwert können verwendet werden, um personalisierte Empfehlungen für Benutzer zu erstellen.
Zeitreihensanalyse: Der Median, Modus und Mittelwert können verwendet werden, um Trends in Zeitreihendaten zu erkennen.
Natürliche Sprachverarbeitung: Der Median, Modus und Mittelwert können verwendet werden, um die Bedeutung von Text zu verstehen.

Beispiel: Wir haben die Geschwindigkeit von 13 Autos registriert:

geschwindigkeit = [99,86,87,88,111,86,103,87,94,78,77,85,86]

Was ist der durchschnittliche, der mittlere oder der häufigste Geschwindigkeitswert?

Mittelwert

Der Mittelwert ist der Durchschnittswert.

Um den Mittelwert zu berechnen, ermitteln wir die Summe aller Werte und dividieren die Summe durch die Anzahl der Werte:

(99+86+87+88+111+86+103+87+94+78+77+85+86) / 13 = 89.77

Das NumPy-Modul verfügt hierfür über eine Methode.

Wir verwenden die NumPy mean()-Methode, um die Durchschnittsgeschwindigkeit zu ermitteln:

import numpy

geschwindigkeit = [99,86,87,88,111,86,103,87,94,78,77,85,86]

x = numpy.mean(geschwindigkeit)

print(x)

Beispiel des Mittelwerts

Datensatz: Angenommen, wir haben die folgenden Noten für eine Prüfung in einer Klasse von 20 Schülern:

12 Punkte
14 Punkte
15 Punkte
16 Punkte
17 Punkte
18 Punkte
19 Punkte
20 Punkte

Fragestellung:

Wie hoch ist die durchschnittliche Note in der Prüfung?

Mittelwert:

Der Mittelwert der Noten in diesem Datensatz beträgt 16,5 Punkte.

Berechnung:

Der Mittelwert wird berechnet, indem man die Summe aller Werte durch die Anzahl der Werte dividiert. In diesem Fall:

(12 + 14 + 15 + 16 + 17 + 18 + 19 + 20) / 20 = 16,5

Interpretation:

Die durchschnittliche Note in der Prüfung liegt bei 16,5 Punkten.

Weitere Anwendungsbereiche:

Der Mittelwert kann in vielen weiteren Bereichen eingesetzt werden, z. B.:

Berechnung des Durchschnittseinkommens: Der Mittelwert kann verwendet werden, um das Durchschnittseinkommen einer Bevölkerungsgruppe zu berechnen.
Vergleich von zwei Gruppen: Der Mittelwert kann verwendet werden, um zwei Gruppen zu vergleichen, z. B. die Schuhgrößen von Jungen und Mädchen in einer Klasse.
Berechnung von Wahrscheinlichkeiten: Der Mittelwert kann verwendet werden, um Wahrscheinlichkeiten zu berechnen, z. B. die Wahrscheinlichkeit, dass eine Person eine bestimmte Krankheit hat.

Fazit:

Der Mittelwert ist ein wichtiges Lagemaß, das in vielen Bereichen des Machine Learnings und der Statistik verwendet wird. Er ist besonders nützlich, wenn man das arithmetische Mittel einer Reihe von Werten berechnen möchte.

Hinweis:

Es ist wichtig zu beachten, dass der Mittelwert empfindlich gegenüber Ausreißern ist. Ein einzelner Ausreißer kann den Mittelwert stark verzerren. In solchen Fällen kann es sinnvoller sein, den Median oder den Modus zu verwenden.

Median

Der Medianwert ist der Wert in der Mitte, nachdem wir alle Werte sortiert haben:

77, 78, 85, 86, 86, 86, 87, 87, 88, 94, 99, 103, 111

Es ist wichtig, dass die Zahlen sortiert werden, bevor Sie den Median ermitteln können. Das NumPy-Modul verfügt hierfür über eine Methode:

Man verwenden die NumPy median()-Methode, um den Mittelwert zu ermitteln:

import numpy

geschwindigkeit = [99,86,87,88,111,86,103,87,94,78,77,85,86]

x = numpy.median(geschwindigkeit)

print(x)

Wenn sich in der Mitte zwei Zahlen befinden, teilen wir die Summe dieser Zahlen durch zwei.

77, 78, 85, 86, 86, 86, 87, 87, 94, 98, 99, 103 (86 + 87) / 2 = 86.5

Verwendung des NumPy-Moduls:

import numpy

geschwindigkeit = [99,86,87,88,86,103,87,94,78,77,85,86]

x = numpy.median(geschwindigkeit)

print(x)

Beispiel für die Anwendung des Medians

Datensatz: Angenommen, wir haben einen Datensatz mit den Gehältern von Softwareentwicklern in Deutschland:

50.000 €
60.000 €
70.000 €
80.000 €
100.000 €
120.000 €
150.000 €

Fragestellung:

Wie hoch ist das typische Gehalt eines Softwareentwicklers in Deutschland?

Mittelwert:

Der Mittelwert der Gehälter in diesem Datensatz beträgt 87.142 €.

Median:

Der Median der Gehälter in diesem Datensatz beträgt 80.000 €.

Interpretation:

Der Median ist in diesem Fall aussagekräftiger als der Mittelwert, da er durch die extremen Werte (100.000 € und 150.000 €) nicht so stark beeinflusst wird. Der Median von 80.000 € gibt uns daher ein besseres Bild vom typischen Gehalt eines Softwareentwicklers in Deutschland.

Weitere Anwendungsbereiche:

Der Median kann in vielen weiteren Bereichen eingesetzt werden, z. B.:

Vergleich von zwei Gruppen: Der Median kann verwendet werden, um zwei Gruppen zu vergleichen, z. B. die Gehälter von Männern und Frauen.
Identifizierung von Ausreißern: Der Median kann verwendet werden, um Ausreißer in einem Datensatz zu identifizieren.
Berechnung von Quantilen: Der Median kann verwendet werden, um Quantilen zu berechnen, z. B. das 25. Quantil und das 75. Quantil.

Fazit:

Der Median ist ein wichtiges Lagemaß, das in vielen Bereichen des Machine Learnings und der Statistik verwendet wird. Er ist besonders nützlich, wenn der Datensatz Ausreißer enthält oder wenn man das typische Verhalten einer Population beschreiben möchte.

Modus

Der Moduswert ist der Wert, der am häufigsten vorkommt:

99, 86, 87, 88, 111, 86, 103, 87, 94, 78, 77, 85, 86 = 86

Das SciPy-Modul verfügt hierfür über eine Methode.

Man verwendet die SciPy- mode()Methode, um die Zahl zu finden, die am häufigsten vorkommt:

from scipy import stats

geschwindigkeit = [99,86,87,88,111,86,103,87,94,78,77,85,86]

x = stats.mode(geschwindigkeit)

print(x)

Beispiel vom Modus

Datensatz: Angenommen, wir haben eine Umfrage unter 100 Personen durchgeführt und sie gefragt, welche Farbe ihre Lieblingsfarbe ist:

Blau (30 Stimmen)
Rot (20 Stimmen)
Grün (15 Stimmen)
Gelb (15 Stimmen)
Lila (10 Stimmen)
Orange (5 Stimmen)

Fragestellung:

Welche Farbe ist die beliebteste Farbe?

Modus:

Der Modus in diesem Datensatz ist Blau, da es die Farbe mit den meisten Stimmen (30) ist.

Interpretation:

Die meisten Personen in der Umfrage haben Blau als ihre Lieblingsfarbe angegeben. Daher ist Blau die beliebteste Farbe in dieser Stichprobe.

Weitere Anwendungsbereiche:

Der Modus kann in vielen weiteren Bereichen eingesetzt werden, z. B.:

Analyse von Textdaten: Der Modus kann verwendet werden, um die häufigsten Wörter oder Phrasen in einem Text zu finden.
Bildverarbeitung: Der Modus kann verwendet werden, um die häufigste Farbe in einem Bild zu finden.
Clusteranalyse: Der Modus kann verwendet werden, um Cluster von Datenpunkten zu finden, die ähnliche Eigenschaften haben.

Fazit:

Der Modus ist ein wichtiges Lagemaß, das in vielen Bereichen des Machine Learnings und der Statistik verwendet wird. Er ist besonders nützlich, wenn man die häufigste Ausprägung eines Merkmals in einem Datensatz bestimmen möchte.

Hinweis:

Es ist wichtig zu beachten, dass der Modus nicht immer ein eindeutiges Ergebnis liefert. In einigen Fällen kann es mehrere Modi geben, z. B. wenn zwei oder mehr Merkmale die gleiche Anzahl von Stimmen haben.

Zusammenfassung

Mittelwert, Median und Modus sind Techniken, die häufig beim maschinellen Lernen verwendet werden. Daher ist es wichtig, das Konzept dahinter zu verstehen.

Aufgabe

Aufgabe 1: Berechnung des Mittelwerts

Ziel: Schreibe eine Funktion in Python, die den Mittelwert (Durchschnitt) einer Liste von Zahlen berechnet.

Anforderungen:

Die Funktion sollte berechne_mittelwert heißen und eine Liste von Zahlen als Argument akzeptieren.
Die Funktion gibt den Mittelwert dieser Zahlen zurück.
Teste deine Funktion mit der Liste [8, 2, 5, 1, 10].

Aufgabe 2: Berechnung des Medians

Ziel: Implementiere eine Funktion in Python, die den Median einer Liste von Zahlen findet.

Anforderungen:

Benenne die Funktion berechne_median.
Die Funktion soll eine Liste von Zahlen entgegennehmen und den Median zurückgeben.
Für Listen mit einer ungeraden Anzahl von Elementen ist der Median der mittlere Wert, nachdem die Liste sortiert wurde. Bei einer geraden Anzahl von Elementen ist der Median der Durchschnitt der beiden mittleren Werte.
Teste deine Funktion mit den Listen [7, 5, 3, 5] und [1, 2, 3, 4, 5].

Aufgabe 3: Berechnung des Modus

Ziel: Schreibe eine Funktion, die den Modus einer Liste von Zahlen findet.

Anforderungen:

Die Funktion sollte berechne_modus heißen.
Sie sollte den Wert (oder die Werte bei einem Mehrfachmodus) zurückgeben, der in der Liste am häufigsten vorkommt.
Falls alle Werte gleich häufig vorkommen, kann die Funktion entweder alle Werte oder einen Hinweis darauf zurückgeben, dass kein Modus existiert.
Teste die Funktion mit der Liste [4, 1, 2, 2, 3, 1].

Aufgabe 4: Kombinierte Statistik-Funktion

Ziel: Erstelle eine Funktion, die den Mittelwert, Median und Modus einer Liste von Zahlen als Tupel zurückgibt.

Anforderungen:

Die Funktion soll kombinierte_statistik heißen.
Sie nimmt eine Liste von Zahlen als Argument und gibt ein Tupel zurück, das den Mittelwert, Median und Modus in dieser Reihenfolge enthält.
Verwende die Funktionen, die du in den vorherigen Aufgaben geschrieben hast.
Teste deine Funktion mit der Liste [1, 2, 3, 4, 4, 5, 5, 5].

Aufgabe 5: Datenfilterung vor der Berechnung

Ziel: Schreibe eine Funktion, die Zahlen außerhalb eines angegebenen Bereichs entfernt und dann den Mittelwert, Median und Modus der verbleibenden Zahlen berechnet.

Anforderungen:

Die Funktion sollte filter_und_statistik heißen.
Sie nimmt drei Argumente: eine Liste von Zahlen, einen minimalen Wert und einen maximalen Wert. Nur Zahlen innerhalb dieses Bereichs (einschließlich der Grenzen) sollten für die statistischen Berechnungen berücksichtigt werden.
Die Funktion gibt ein Tupel mit dem Mittelwert, Median und Modus der gefilterten Liste zurück.
Teste die Funktion mit der Liste [10, 20, 30, 40, 50, 60, 70], einem minimalen Wert von 20 und einem maximalen Wert von 60.

Standardabweichung

Die Standardabweichung ist eine Zahl, die beschreibt, wie weit die Werte verteilt sind. Eine geringe Standardabweichung bedeutet, dass die meisten Zahlen nahe am Mittelwert liegen. Eine hohe Standardabweichung bedeutet, dass die Werte über einen größeren Bereich verteilt sind.

Beispiel: Diesmal haben wir die Geschwindigkeit von 7 Autos registriert:

geschwindigkeit = [86,87,88,86,87,85,86]

Die Standardabweichung beträgt:

0.9

Dies bedeutet, dass die meisten Werte im Bereich von 0,9 vom Mittelwert liegen Wert, der 86,4 beträgt.

Machen wir dasselbe mit einer Auswahl von Zahlen mit einem größeren Bereich:

geschwindigkeit = [32,111,138,28,59,77,97]

Die Standardabweichung beträgt:

37.85

Dies bedeutet, dass die meisten Werte im Bereich von 37,85 vom Mittelwert liegen Wert, der 77,4 beträgt. Wie man sehen kann, weist eine höhere Standardabweichung darauf hin, dass die Werte über einen größeren Bereich verteilt sind.

Das NumPy-Modul verfügt über eine Methode zur Berechnung der Standardabweichung.

Man verwendet die NumPy std()Methode, um die Standardabweichung zu finden:

import numpy

geschwindigkeitStadtmitte = [86,87,88,86,87,85,86]
geschwindigkeitLandstraße = [32,111,138,28,59,77,97]

x = numpy.std(geschwindigkeitStadtmitte)
y = numpy.std(geschwindigkeitLandstraße)

print(x)

Varianz

Varianz ist eine weitere Zahl, die angibt, wie weit die Werte verteilt sind.

Tatsächlich erhält man die Standardabweichung, wenn man die Quadratwurzel aus der Varianz zieht. Oder umgekehrt: Wenn wir die Standardabweichung mit sich selbst multiplizieren, erhalten wir die Varianz.

Um die Varianz zu berechnen, müssen wir wie folgt vorgehen:

1. Ermittelung des Mittelwerts:

(32+111+138+28+59+77+97) / 7 = 77.4

2. Finden einer Differenz zum Mittelwert bei jedem einzlenen Wert:

32 - 77.4 = -45.4 111 - 77.4 = 33.6 138 - 77.4 = 60.6 28 - 77.4 = -49.4 59 - 77.4 = -18.4 77 - 77.4 = - 0.4 97 - 77.4 = 19.6

3. Für jede Differenz: Ermittlung des Quadratwerts:

(-45.4)² = 2061.16
(33.6)² = 1128.96
(60.6)² = 3672.36
(-49.4)² = 2440.36
(-18.4)² = 338.56
(- 0.4)² = 0.16
(19.6)² = 384.16

4. Die Varianz ist die durchschnittliche Anzahl dieser quadrierten Differenzen

(2061.16+1128.96+3672.36+2440.36+338.56+0.16+384.16) / 7 = 1432.2

Zum Glück verfügt NumPy über eine Methode zur Berechnung der Varianz.

Man verwendet NumPy var()Methode zur Bestimmung der Varianz:

import numpy

geschwindigkeit = [32,111,138,28,59,77,97]

x = numpy.var(geschwindigkeit)

print(x)

Standardabweichung

Wie wir gelernt haben, ist die Formel zur Ermittlung der Standardabweichung die Quadratwurzel der Varianz:

√ 1432.25 = 37.85

Oder man verwendet, wie im vorherigen Beispiel, NumPy, um die Standardabweichung zu berechnen.

Wir verwenden NumPy std()Methode zum Ermitteln der Standardabweichung:

import numpy

geschwindigkeit = [32,111,138,28,59,77,97]

x = numpy.std(geschwindigkeit)

print(x)

Symbole

Die Standardabweichung wird oft durch das Symbol Sigma: σ dargestellt

Varianz wird oft durch das Symbol Sigma-Quadrat dargestellt: σ ²

Zusammenfassung

Standardabweichung und Varianz sind Begriffe, die beim maschinellen Lernen häufig verwendet werden. Daher ist es wichtig zu verstehen, wie man sie erhält und welches Konzept dahinter steckt.

Hinweis: Die Standardabweichung gibt an, wie weit die Zahlen im Durchschnitt vom Mittelwert der Liste entfernt sind. Sie ist ein Maß für die Streuung der Daten.

Aufgabe

Aufgabe 1: Berechnung der Varianz

Ziel: Schreibe eine Funktion in Python, die die Varianz einer Liste von Zahlen berechnet.

Anforderungen:

Die Funktion sollte berechne_varianz heißen und eine Liste von Zahlen als Argument akzeptieren.
Berechne zuerst den Mittelwert der Liste.
Verwende den Mittelwert, um die Varianz zu berechnen, indem du die quadratische Abweichung jeder Zahl vom Mittelwert summierst, dann die Summe durch die Anzahl der Elemente in der Liste teilst.
Die Funktion gibt die Varianz dieser Zahlen zurück.
Teste deine Funktion mit der Liste [4, 8, 6, 5, 3, 2].

Hinweis: Die Varianz misst die Streuung der Zahlen in der Liste um ihren Mittelwert.

Aufgabe 2: Berechnung der Standardabweichung

Ziel: Implementiere eine Funktion in Python, die die Standardabweichung einer Liste von Zahlen findet.

Anforderungen:

Benenne die Funktion berechne_standardabweichung.
Die Funktion soll eine Liste von Zahlen entgegennehmen.
Verwende die Funktion berechne_varianz aus der vorherigen Aufgabe, um die Varianz der Liste zu berechnen.
Berechne die Standardabweichung, indem du die Quadratwurzel der Varianz ermittelst. Du kannst die Funktion sqrt aus dem Modul math verwenden, um die Quadratwurzel zu berechnen.
Die Funktion gibt die Standardabweichung der Liste zurück.
Teste deine Funktion mit der Liste [9, 2, 5, 4, 12, 7, 8, 11].

Perzentile

Perzentile werden in Statistiken verwendet, um eine Zahl auszugeben, die einen Wert beschreibt, unter welchem ein bestimmter Prozentsatz an Werten in einer Sammlung von Messdaten liegt.

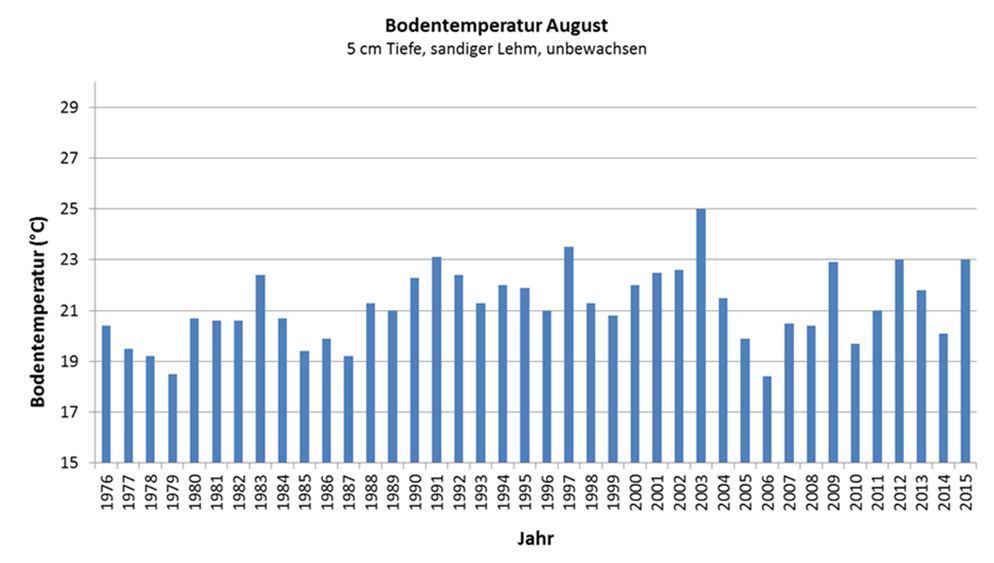
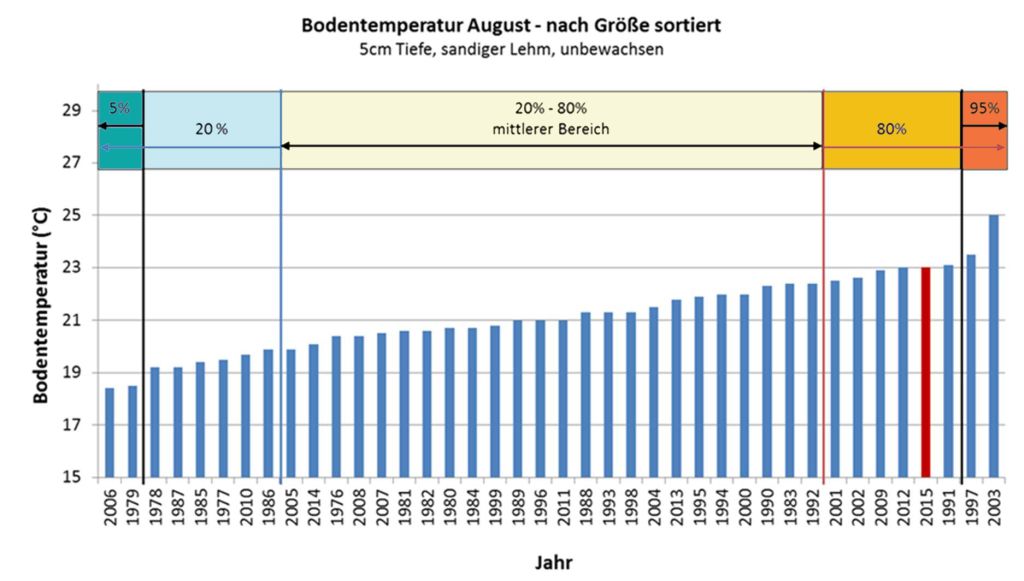
Beispiel: Nehmen wir an, wir haben eine Liste mit dem Alter aller Menschen, die in einer Straße leben.

alter = [5,31,43,48,50,41,7,11,15,39,80,82,32,2,8,6,25,36,27,61,31]

Was ist das 75. Perzentil? Die Antwort ist 43, was bedeutet, dass 75 % der Menschen 43 Jahre oder jünger sind.

In NumPy haben wir eine Methode zum Ermitteln des angegebenen Perzentils: Hierfür verwenden wir die percentile()Methode zum finden von Perzentilen:

import numpy

alter = [5,31,43,48,50,41,7,11,15,39,80,82,32,2,8,6,25,36,27,61,31]

x = numpy.percentile(alter, 75)

print(x)

Unter welchem Alter sind 90 % der Menschen jünger?

import numpy

alter = [5,31,43,48,50,41,7,11,15,39,80,82,32,2,8,6,25,36,27,61,31]

x = numpy.percentile(alter, 90)

print(x)

Aufgabe

Berechnung von Perzentile

Schreibe eine Funktion in Python, das 75. Perzentil der Schulwegstrecke aller Klassenkameraden ausgibt.